SIMULATION DE LA TRAJECTOIRE D'UNE PARTICULE CHARGEE DANS UN CHAMP MAGNÉTIQUE

> restart;

Appliquons le pricipe fondamental de la dynamique à une particule chargée:

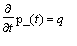.V_^ B_

On projette les équations sur les trois axes du repère cartésien:

Sur x_:

> eqd1:=m*diff(vx(t),t)=q*vy(t)*B;

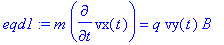
Sur y_:

> eqd2:=m*diff(vy(t),t)=-q*vx(t)*B;

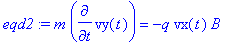
Sur z_:

> eqd3:=m*diff(vz(t),t)=0;

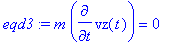
On prend les conditions initiales suivantes: vy(0)=0,vx(0)=vo,vz(0)=vo

> eqns := {eqd1, eqd2, eqd3,vy(0)=0,vx(0)=vo,vz(0)=vo}:

> sol := dsolve( eqns,{vx(t),vy(t),vz(t)});

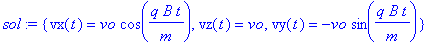
On pose 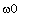=q.B/m

> readlib(isolate):

> eq:=omega0=q*B/m;

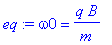
> assign(isolate(eq,B));

> sol;

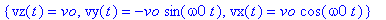
> assign(sol);

> rx:=int(vx(t),t);ry:=int(vy(t),t);rz:=int(vz(t),t);

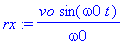
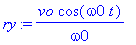
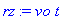
On passe rx, ry et rz en fonctionnel

> rx:=(t,vo,omega0)->vo*sin(omega0*t)/omega0;

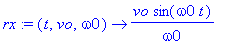
> ry:=(t,vo,omega0)->vo*cos(omega0*t)/omega0;

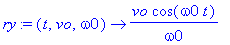
> rz:=(t,vo,omega0)->vo*t;

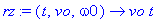
Pour un ion

> omega1:=e*B/mi;

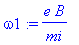
Pour un électron

> omega2:=e*B/me;

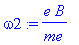
Veleurs numériques

> me:=9.1*10^(-31):mi:=2*1.6*10^(-27):ve:=5.7*10^7:vi:=9.8*10^5:B:=6:e:=1.6*10^(-19):c:=3*10^8:

Si on se place dans le cadre relativiste, il faut substituer 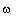par /

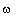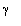
> gamma1:=1/(1-vi^2/c^2)^(1/2);

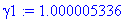
> gamma2:=1/(1-ve^2/c^2)^(1/2);

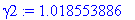
Etant très proches de 1, on ne se placera pas dans l'hypothèse relativiste

> spacecurve([rx(t,vi,omega1),ry(t,vi,omega1),t],t=0..8*Pi/omega1,axes=normal,numpoints=200,title="Mouvement d'un ion positif le long d'une ligne de champ magnétique",color=blue);

> spacecurve([rx(t,ve,omega2),ry(t,ve,omega2),t],t=0..8*Pi/omega2,axes=normal,numpoints=200,title="Mouvement d'un électron le long d'une ligne de champ magnétique",color=red);

> p1:=spacecurve([rx(t,vi,omega1),ry(t,vi,omega1),t],t=0..2*Pi/omega1,axes=normal,numpoints=200,color=blue):

> p2:=spacecurve([rx(t,ve,omega2),ry(t,ve,omega2),t],t=0..2*Pi/omega1,axes=normal,numpoints=500,color=red):

> display3d([p1,p2],title="Mouvement d'un électron et d'un ion positif le long d'une ligne de champ magnétique. B_=B(z).uz_",axes=normal);

Si l'on considère le plan orthogonal à z_, le mouvement est circulaire de rayon R. Ce dernier est appellé rayon de Larmor.

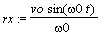
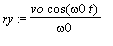
Donc

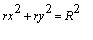
Par identification

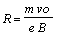
> R:=(m,vo)->m*vo/e/B;

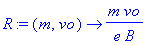
Application numérique:

Pour un électron

> R(me,ve);

Pour un ion

> R(mi,vi);

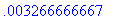
> R(mi,vi)/R(me,ve);

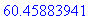
Les rayon de Larmor d'un ion est donc environ 50 fois plus grand que celui d'un électron

La fréquence de giration autour des lignes de champ est différente selon l'espèce:

Pour un électron

> f1:=omega1/(2*Pi):
evalf(f1);

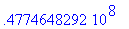
Pour un ion

> f2:=omega2/(2*Pi):
evalf(f2);

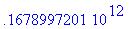
> f2/f1;

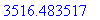
Les électrons tournent donc à une fréquence environ 3000 fois supérieure à celle des ions